If LSJL can physically deform the bone then perhaps it can deform the bone in such a way as to make it longer.

Creep of trabecular bone from the human proximal tibia

“Creep is the deformation that occurs under a prolonged, sustained load and can lead to permanent damage in bone{So to get creep with LSJL the duration of the loads should be longer}. Creep in bone is a complex phenomenon and varies with type of loading and local mechanical properties. Human trabecular bone samples from proximal tibia were harvested from a 71-year old female cadaver with osteoporosis. The samples were initially subjected to one cycle load up to 1% strain to determine the creep load. Samples were then loaded in compression under a constant stress for 2 h and immediately unloaded. All tests were conducted with the specimens soaked in phosphate buffered saline with proteinase inhibitors at 37 °C. Steady state creep rate and final creep strain were estimated from mechanical testing and compared with published data. The steady state creep rate correlated well with values obtained from bovine tibial and human vertebral trabecular bone, and was higher for lower density samples. Tissue architecture was analyzed by micro-computed tomography (μCT) both before and after creep testing to assess creep deformation and damage accumulated. Quantitative morphometric analysis indicated that creep induced changes in trabecular separation and the structural model index. A main mode of deformation was bending of trabeculae{stretchinig of the trabeculae would be what would make it longer although it’s possible that bending would make trabeculae longer if done in a certain way}.”

” One manifestation of creep damage is the decreased stature of elderly individuals due to the creep damage of vertebrae”

” trabeculae from vertebral areas are mostly rod-like, while in the metaphyses and epiphyses of long bones there is a more balanced mixture of plate-like and rod-like trabeculae. Furthermore, it was shown that these cellular structures degrade differently during the progression of osteoporosis, resulting in differences in the degree of anisotropy of mechanical properties”

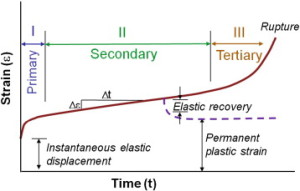
” Creep occurs in three stages: primary, secondary and tertiary. Primary creep is the brief initial period during which the creep rate decreases and is accompanied with some material relaxation. In secondary creep, which is the longest and most studied regime, a steady state creep rate (dε/dt) is observed. Tertiary creep, occurring at the end of the secondary regime, is associated with an accelerated creep rate and more damage accumulation that results in eventual failure if the load is sustained. If the creep test is stopped during the secondary stage and the load removed, there is some elastic and viscoelastic strain recovery.”

“under a prolonged load, microcracking of the bone matrix (and not fracture of the whole trabeculae) was the primary mode of deformation during creep. On the other hand, it was shown that even a small damage, barely distinguished on radiographs, to older vertebrae accelerates creep, and leads to a visible contribution to a vertebra deformity”

Here’s a paper that shows possible positive benefits of creep deformation:

In vitro torsion-induced stress distribution changes in porcine intervertebral discs.

“A cadaveric porcine spine motion segment experiment was conducted.

To test the hypothesis that small vertebral rotations cause increased stress in the anulus while decreasing stress in the nucleus through stiffening of the anulus.

Stress profiles of the intervertebral disc reportedly depend on degeneration grade and external loading. Increased stress in the anulus was found during asymmetric loading. In addition, depressurization of the nucleus combined with an instantaneous disc height increase was found when small (<2 degrees ) axial vertebral rotations were applied{So twisting could increasing height?}.

Seven lumbar porcine cadaveric motion segments consisting of two vertebrae and the intervening disc with ligaments were loaded in the neutral position with 340 N of compression. Stress profiles were obtained in the neutral position, then after 0.5 degrees and 1 degrees axial rotation of the bottom vertebral body. The distribution of compressive stress in the disc matrix was measured by pulling a miniature pressure transducer through the disc along a straight path in the midfrontal plane. Stress profiles were measured in vertical (0 degrees ) and horizontal (90 degrees ) orientation.

Deformation of the anulus by small axial rotations of the lower vertebra instantaneously decreased the horizontally and vertically measured stress in the nucleus while increasing stress in the anulus. A 1-hour period of creep loading decreased the stresses in the nucleus and the anulus 20% to 30%, depending on the orientation, but the effect of an increasing stress in the anular region after axial rotation persisted.

The compressive Young’s modulus of the composite anulus tissue increases instantaneously when small axial rotations are applied to porcine spine motion segments. This is accompanied by decreased stress in the nucleus pulposus, increased stress in the anulus fibrosus, changes in the stress profile superimposed on and independent of prolonged viscoelastic creep and dehydration, and changes in stress distribution independent of horizontal and vertical orientation.”

“the nucleus acts as a sealed hydraulic system, in which the fluid pressure rises substantially when volume is increased (by fluid injection) and falls when volume is decreased (by surgical excision or endplate fracture). “Stress” peaks in the anulus reportedly are increased by prior loading and degeneration.”

“[The] pressure reduction in the nucleus pulposus under torsion coincided with an increase of disc height ”

Magnitude of loads influences the site of failure of highly curved bones.

“The structure and material properties of bones along with applied boundary conditions determine the region of peak stresses, where fracture is expected to occur. As the site of peak stresses is not influenced by the magnitude of applied load, the fracture site is not expected to change during fatigue loading of whole bone at different loads. However, in a highly curved bone such as the rat ulna, the magnitude of applied loads was found to influence the fracture site. Fatigue loading was conducted under load control on intact rat forearms and on excised ulnae. The distance to the site of failure from the proximal olecranon process of ulnae was determined. In intact forearms, the site of failure demonstrated a linear progression distally, towards sites with lower moment of inertia (or sites exhibiting lower section modulus). Intact rat forearms and excised ulnae loaded to failure at low loads fractured 2-3mm distal to where they failed when applying high loads. This indicates a shift in the site of failure by approximately 10% of whole bone length just by varying the applied load magnitude. The site of failure in excised ulnae was similar when loading at 2Hz or at 4Hz, suggesting that this was frequency independent in this range and indicating that strain rate was not an important contributing factor. Creep loading of excised ulnae also demonstrated similar changes in the site of failure, indicating that magnitude of loads, and not type of loading were important in determining the site of failure.”

“the shape of whole bone can be such that failure occurs at sites other than the smallest cross-section and/or smallest moment of inertia. This is especially true for curved bones such as the ulnae and tibiae of commonly used rodent strains.”

“Loading was conducted by placing the excised ulnae between brass U-cups, with the load being applied in the direction parallel to the length of the ulna (left-to-right). During this loading, the natural curvature of the ulna causes bending induced tensile and compressive stresses on the lateral and medial surfaces, respectively”

“a gradual shift is observed as the site of failure of the ulna moves from 15.2 mm to 17.3 mm as the peak compressive load decreases from 26 N to 14 N”

“In excised ulnae, the site of failure shifted distally as the load was decreased, with failure occurring slightly distal to the mid-shaft at high loads and even more distally at lower loads, irrespective of the frequency of cyclic loading (2 Hz or 4 Hz) or the mode of loading (creep or cyclic).”

“Failure occurred at extremely short time scales at high loads, and at considerably longer time scales when loading at low loads. When loading at high loads, times to failure were not dependent on loading frequency or mode of loading (creep or cyclic). When loading at low loads, the time it took for the bones to fail decreased with increased frequency of cyclic loading  and was the shortest during creep loading. Dring cyclic loading, failure occurs in fewer cycles at greater loads, irrespective of the frequency of loading. At the same loads, loading at a higher frequency (2 Hz vs 4 Hz), there was no difference in the numbers of cycles to failure when loading was conducted at different frequencies (2 Hz or 4 Hz).”

“As expected, loading at high loads causes bones to fail in shorter times (within 30 s) as opposed to loading at low loads (periods of a week or two).”<-Loading for a week or two would be extreme.